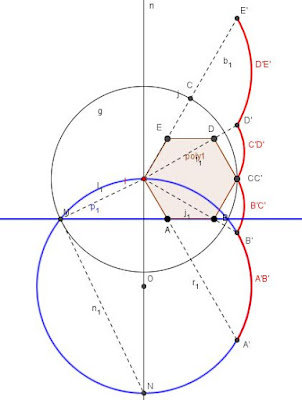
El primer paso consiste en localizar las inversas de cada uno de los lados del hexágono. Comenzamos por el lado C-D. Este lado pertenece a una recta que no contiene el centro de inversión (I) representado de color azul. Por tanto su inversa es una circunferencia que sí contiene el centro (I), y cuyo centro se encuentra en la perpendicular desde el centro de inversión a la recta que contiene el lado. Conociendo la circunferencia de autoinversión calculamos D', el inverso del punto D. Trazamos la circunferencia inversa de diámetro I-D'. Dentro de esta circunferencia trazamos de rojo el arco de circunferencia que se corresponde con el lado C-D
A continuación trazamos la circunferencia inversa de la recta que contiene el lado D-E. De igual forma que el paso anterior, calculamos el arco de circunferencia correspondiente a los vértices D'-E'
De forma similar calculamos los lados B'-C'
A continuación procedemos con el arco de circunferencia A'-B' inverso al lado A-B
Como podemos observar los puntos inversos se encuentran alineados. Como hemos comentado al inicio, estos vértices se inscriben en una circunferencia que contiene el centro de inversión, por lo que los vértices inversos pertenecen a una recta perpendicular al diámetro de la misma que pasa por el centro y el centro de inversión.
Finalmente trazamos el área infinita del hexágono inverso.






No hay comentarios:
Publicar un comentario